Описание массивов
Описание массивов
Как структура представления массив является упорядоченным множеством элементов определенного типа. Упорядоченность массива определяется набором целых чисел, называемых индексами, которые связываются с каждым элементом массива и однозначно определяют его расположение среди других элементов массива. Локализация конкретного элемента массива — ключевая задача при разработке любых алгоритмов, работающих с массивами. Ее сложность прямо зависит от размерности массива.
Наиболее просто представляются одномерные массивы. Соответствующая им структура хранения — это вектор. Она однозначна и представляет собой просто последовательное расположение элементов в памяти. Чтобы локализовать нужный элемент одномерного массива, достаточно знать его индекс. Так как ассемблер не имеет средств для работы с массивом как структурой данных, то для использования элемента массива необходимо вычислить его адрес. Для вычисления адреса i-ro элемента одномерного массива можно использовать формулу:
Аi=АБ+i*lеn
Здесь АБ — адрес первого элемента массива размерностью n, i — индекс (i=0.. n-1), len — размер элемента массива в байтах. Заметьте, что при таком определении можно не говорить о типе элементов массива. В общем случае они также могут быть структурированными объектами данных.
Представление двумерных массивов немного сложнее. Здесь мы имеем случай, когда структуры хранения и представления различны. О структуре представления говорить излишне — это матрица. Структура хранения остается прежней — вектор. Но теперь его нельзя без специальных оговорок интерпретировать однозначно. Все зависит от того, как решил разработчик программы «вытянуть» массив — по строкам или по столбцам. Наиболее естествен порядок расположения элементов массива — по строкам. При этом наиболее быстро изменяется последний элемент индекса. К примеру, рассмотрим представление на логическом уровне двумерного массива Ац размерностью nxm, где 0 < i < n—I, 0 < j < m-1:
а00 а01 а02 а03
а10 а11 а12 а13
а20 а21 а22 а23
а30 а31 а32 а33
Соответствующее этому массиву физическое представление в памяти — вектор — будет выглядеть так:
а00 а01 а02 а03а10 а11 а12 а13а20 а21 а22 а23а30 а31 а32 а33
Номер конкретного элемента массива в этой, уже как бы ставшей линейной, последовательности определяется адресной функцией, которая устанавливает положение (адрес) в памяти этого элемента исходя из значения его индексов:
aij=n*i + j.
Для получения адреса элемента массива в памяти необходимо полученное значение умножить на размер элемента и сложить с базовым адресом массива.
Аналогично осуществляется локализация элементов в массивах большей размерности. На Рисунок 2.1 показан трехмерный массив Aijz размерностью n x m x к, где n = 4, m = 4, к = 2.
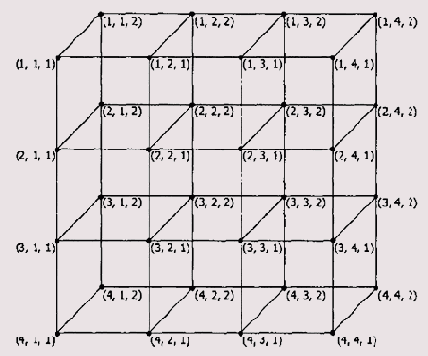
Рисунок 2.1. Пример логической структуры трехмерного массива
Cоответствующий этому массиву вектор памяти будет выглядеть так:а120
а000 а001 а010а011а020 а021 а030 а031а100 а101 а111 а120.. а331
Соответственно номер элемента определяется так:
aijz=n*m*i + m*j + z, где 0 < i < n-1, 0 < j < m-1, 0 < z < k-1.
Для получения адреса осталось умножить полученное значение на размер элемента массива и сложить результат с базовым адресом массива.
Таким образом, преобразование многомерной, в общем случае логической структуры массива в одномерную физическую структуру производится путем ее линеаризации по строкам или столбцам. В первом случае, быстрее всего изменяется последний индекс каждого элемента, во втором — первый индекс. Недостаток описанного способа локализации элемента массива в том, что процесс вычисления адреса подразумевает выполнение операций сложения и умножения. Как известно, они не являются быстрыми. Существует метод Дж. Айлиффа, с помощью которого можно исключить операцию умножения из процесса вычисления индекса. Индексация в массиве производится с помощью иерархии дескрипторов, называемых векторами Айлиффа, так как это показано на Рисунок 2.2. На этом рисунке j,, )ь j3 обозначают соответственно первый, второй и третий индексы массива.
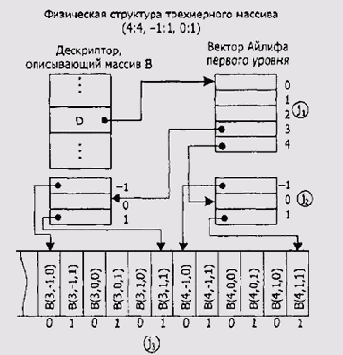
Рисунок 2.2. Представление предыдущего трехмерного массива по методу Айлиффа
Из рисунка видно, что основной дескриптор массива содержит указатель на вектор Айлиффа первого уровня. Вектор первого уровня является единственным и содержит указатели векторов Айлиффа следующего уровня. То есть, иерархия дескрипторов однозначно отражает размерность массива. Локализовать нужный элемент массива можно, руководствуясь его индексом логического уровня. Для этого нужно пройти по цепочке от основного дескриптора через соответствующие элементы векторов Айлиффа, извлекая из них и суммируя значения смещений с базовым адресом массива:
Здесь (D) — значение указателя вектора Айлиффа первого уровня, хранящееся в основном дескрипторе. При необходимости никто не мешает вам разместить в элементах векторов Айлиффа и другую служебную информацию, например диапазон изменения соответствующего индекса. Очевидный недостаток метода Айлиффа — увеличение общего объема памяти для структуры хранения многомерного массива в памяти.
Что касается описания массива в программе на ассемблере, то его варианты были подробно рассмотрены в учебнике. Перечислим их очень конспективно:
После рассмотрения возможностей по динамическому выделению памяти в операционных средах MS DOS и Windows можно к перечисленным трем вариантам добавить еще один — динамическое распределение памяти. Применительно к программированию для Windows возможности здесь очень широкие и можно использовать наиболее подходящий способ из трех, обсуждавшихся в разделе «Способы распределения памяти».
Массив в разное время работы с ним может изменять свои характеристики — имя массива, адрес в памяти первого его элемента, количество и диапазон изменения индексов, тип элементов, размерность и т. п. В этом случае имеет смысл его физическое представление в памяти предварять специальным заголовком, или дескриптором, в котором указывать характеристики массива, чтобы программа могла правильно обрабатывать элементы массива. Особенно это важно, когда память для массива выделяется динамически.